Monte Carlo Control Methods

Date: 2018-07-01

In this notebook, we cover Monte Carlo control methods where our task is to find the optimal policy to solve Black Jack.

A Cartoon image of Monte Carlo Control:

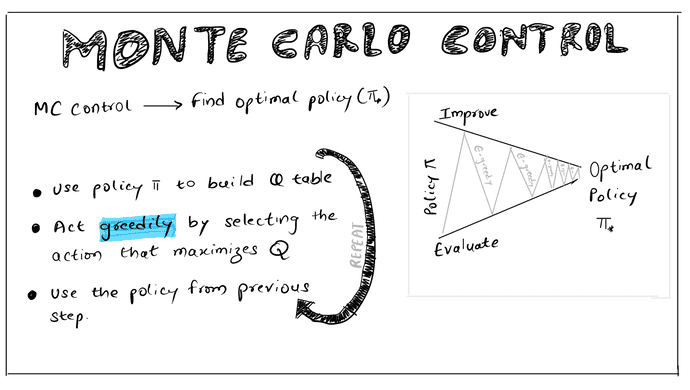
See Also

Temporal Difference Methods ➡️ Part 1: SARSA | Part 2: SARSAMAX | Part 3: EXPECTED SARSA

Import Libraries

import sys
from collections import defaultdict, deque
import numpy as np
import matplotlib.pyplot as plt
import gym
from plot_utils import plot_blackjack_values, plot_policy

Create Gym Environment

# env = gym.make('FrozenLake8x8-v0')
env = gym.make('Blackjack-v0')

print('state space: {}'.format(env.observation_space))
print('action space: {}'.format(env.action_space))

state space: Tuple(Discrete(32), Discrete(11), Discrete(2))
action space: Discrete(2)

state = env.reset()
while True:
    action = env.action_space.sample()
    next_state, reward, done, info = env.step(action)
    if done:
        print(reward)
        break

Explore-Exploit Dilemma

If the agent chooses to only explore the environment, then it will not learn anything and if it only chooses to exploit, it will learn a sub-optimal policy because it wouldn’t see states that could lead to better policies.

EPSILON-GREEDY

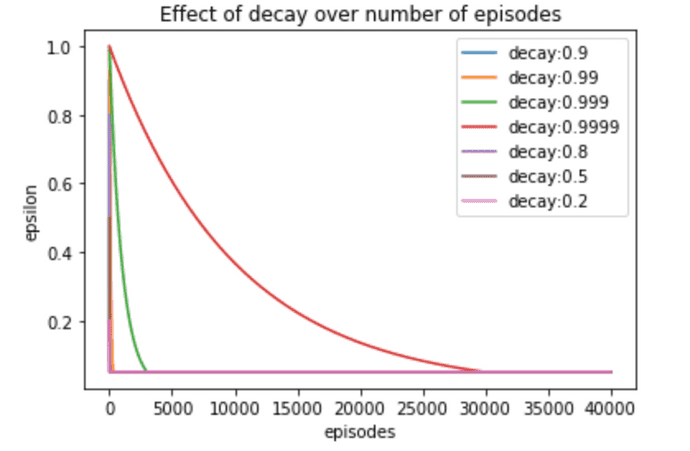
We use epsilon-greedy policy to allow agent do a lot more exploration for initial episodes and, as the agent collects more experience, we decay eps (epsilon) to reduce exploration and increase exploitation. For eps probability, we select action uniformly at random (explore) and for 1-eps probability, we select action that maximises the Q (exploit).

First-Visit Incremental Implementation (W=1)

action-values are estimated after each episode instead of waiting for all episodes to finish.

$\begin{aligned} Q(S_t,A_t) = Q(S_t, A_t) + \frac{1}{N(S_t,A_t)}(G_t - Q(S_t,A_t)) \end{aligned}$

def eps_greedy(env, eps, state, Q):
    rnd = np.random.randn()
    if state in Q:
        if rnd < eps:
            action = env.action_space.sample()
        else:
            action = np.argmax(Q[state])
    else:
        action = env.action_space.sample()
        
    return action

def generate_episode(env, Q, eps):
    state = env.reset()
    episode = []
    while True:
        action = eps_greedy(env, eps, state, Q)
        next_state, reward, done, info = env.step(action)
        episode.append((state, action, reward))
        state = next_state
        if done:
            break
            
    return episode

def first_visit_mc_control_incremental(env, num_episodes, eps=1.0, eps_decay=0.9999, min_eps=0.05, gamma=1.0):
    nA = env.action_space.n
    Q = defaultdict(lambda: np.zeros(nA))
    N = defaultdict(lambda: np.zeros(nA))
    eps = 1.0
    for i in range(1, num_episodes+1):
        if i % 1000 == 0:
            print('\rProgress: {}/{}'.format(i, num_episodes), end="")
            sys.stdout.flush()
            
        eps = max(eps * eps_decay, min_eps)
        
        # Generate episopde
        episode = generate_episode(env, Q, eps)
        
        # Update Q values
        states, actions, rewards = zip(*episode)
        discounts = np.array([gamma ** i for i in range(len(rewards) + 1)])
        N_i = defaultdict(lambda: np.zeros(nA))
        for idx, state in enumerate(states):
            action = actions[idx]
            if N_i[state][action] == 0:
                N_i[state][action] = 1
                N[state][action] += 1
                G = sum(rewards[idx:] * discounts[:-(idx+1)])
                Q[state][action] += 1/N[state][action] * (G - Q[state][action])
                
    policy = {state:np.argmax(actions) for state, actions in Q.items()}
                
    return policy, Q

policy, Q = first_visit_mc_control_incremental(env, 500000)

Progress: 500000/500000

# obtain the corresponding state-value function
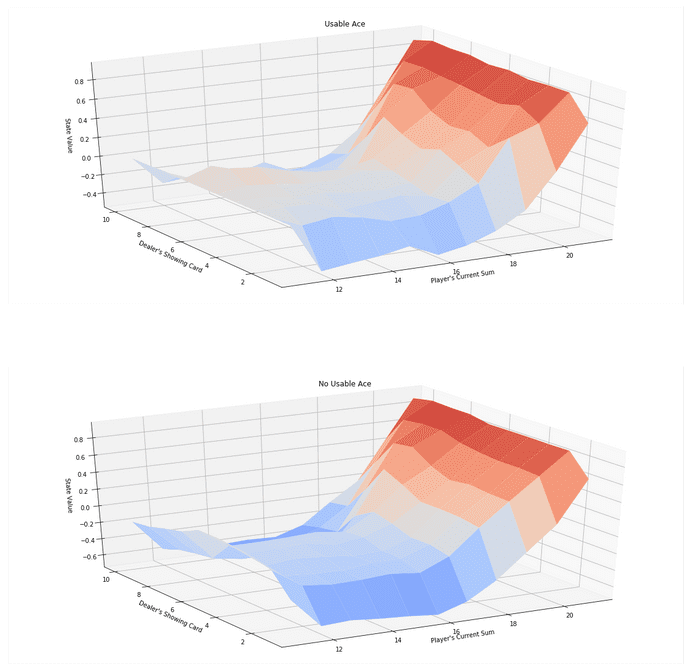
V_to_plot =  {state: np.max(actions) for state, actions in Q.items()}

# plot the state-value function
plot_blackjack_values(V_to_plot)

Every-Visit Incremental

def every_visit_mc_control_incremental(env, num_episodes, eps=1.0, eps_decay=0.9999, min_eps=0.05, gamma=1.0):
    nA = env.action_space.n
    Q = defaultdict(lambda: np.zeros(nA))
    N = defaultdict(lambda: np.zeros(nA))
    eps = 1.0
    for i in range(1, num_episodes+1):
        if i % 1000 == 0:
            print('\rProgress: {}/{}'.format(i, num_episodes), end="")
            sys.stdout.flush()
            
        eps = max(eps * eps_decay, min_eps)
        
        # Generate epispde
        episode = generate_episode(env, Q, eps)
        
        # Update Q values
        states, actions, rewards = zip(*episode)
        discounts = np.array([gamma ** i for i in range(len(rewards) + 1)])
        for idx, state in enumerate(states):
            action = actions[idx]
            N[state][action] += 1
            G = sum(rewards[idx:] * discounts[:-(idx+1)])
            Q[state][action] += 1/N[state][action] * (G - Q[state][action])
                
    policy = {state:np.argmax(actions) for state, actions in Q.items()}
                
    return policy, Q

policy, Q = every_visit_mc_control_incremental(env, 500000)

# obtain the corresponding state-value function
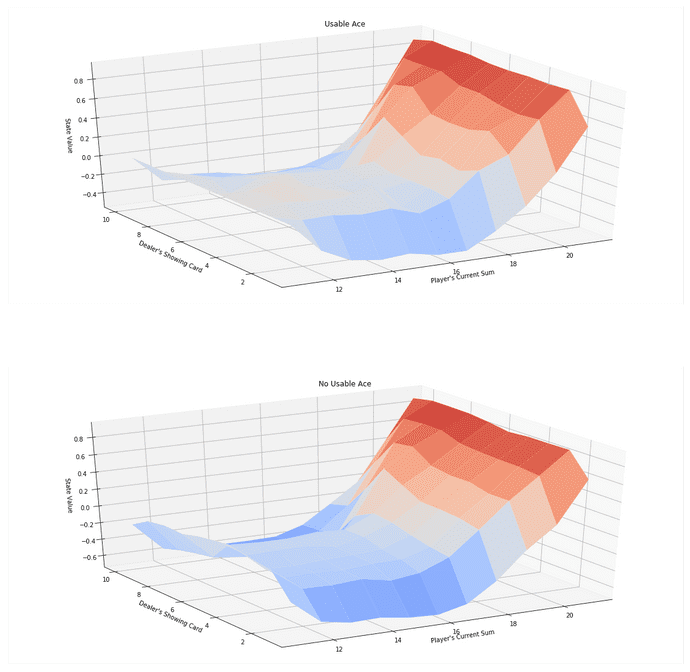
V_to_plot =  {state: np.max(actions) for state, actions in Q.items()}

# plot the state-value function
plot_blackjack_values(V_to_plot)

Progress: 500000/500000

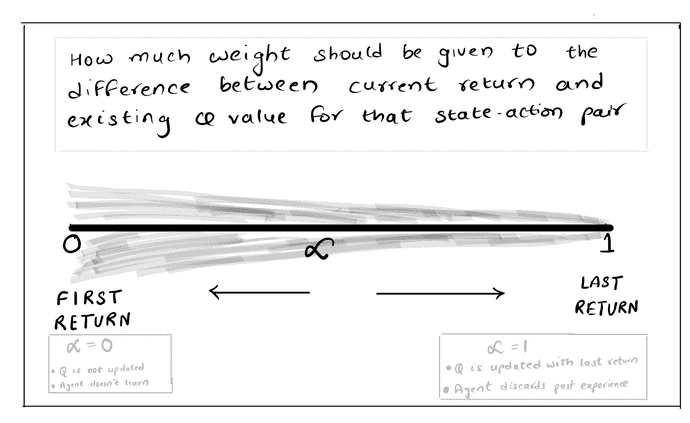
Constant - $\alpha$

With constant-alpha, we introduce another hyperparameter to choose how much weight should be given to the recent returns.

$\begin{aligned} Q(S_t,A_t) = Q(S_t, A_t) + \alpha(G_t - Q(S_t,A_t)) \end{aligned}$

First-Visit $constant\, -\, \alpha$

def first_visit_mc_control_const_alpha(env, num_episodes, eps=1.0, eps_decay=0.9999, eps_min=0.5, alpha=0.01, gamma=1.0):
    nA = env.action_space.n
    Q = defaultdict(lambda: np.zeros(nA))
    
    for i in range(num_episodes):
        if i % 1000 == 0:
            print('\rProgress:{}/{}'.format(i, num_episodes), end="")
            sys.stdout.flush()
        
        eps = max(eps * eps_decay, eps_min)
        episodes = generate_episode(env, Q, eps)
        # Update Q values
        states, actions, rewards = zip(*episodes)
        discounts = np.array([gamma ** i for i in range(len(rewards) + 1)])
        N_i = defaultdict(lambda: np.zeros(nA))
        for idx, state in enumerate(states):
            action = actions[idx]
            if N_i[state][action] == 0:
                N_i[state][action] = 1
                G = sum(rewards[idx:] * discounts[:-(idx+1)])
                Q[state][action] += alpha * (G - Q[state][action])
                
    policy = {state:np.argmax(actions) for state, actions in Q.items()}
                
    return policy, Q

policy, Q = first_visit_mc_control_const_alpha(env, 500000)

# obtain the corresponding state-value function
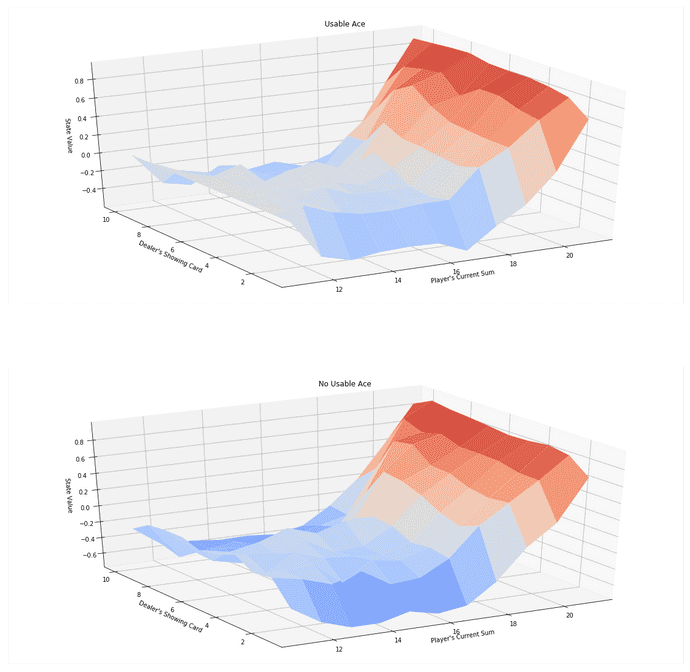
V_to_plot =  {state: np.max(actions) for state, actions in Q.items()}

# plot the state-value function
plot_blackjack_values(V_to_plot)

Progress:499000\500000

Every-Visit $constant \, - \,\alpha$

def every_visit_mc_control_const_alpha(env, num_episodes, eps=1.0, eps_decay=0.99999, eps_min=0.5, alpha=0.01, gamma=1.0):
    nA = env.action_space.n
    Q = defaultdict(lambda: np.zeros(nA))
    
    for i in range(num_episodes):
        if i % 1000 == 0:
            print('\rProgress:{}/{}'.format(i, num_episodes), end="")
            sys.stdout.flush()
        
        eps = max(eps * eps_decay, eps_min)
        episodes = generate_episode(env, Q, eps)
        # Update Q values
        states, actions, rewards = zip(*episodes)
        discounts = np.array([gamma ** i for i in range(len(rewards) + 1)])
        for idx, state in enumerate(states):
            action = actions[idx]
            G = sum(rewards[idx:] * discounts[:-(idx+1)])
            Q[state][action] += alpha * (G - Q[state][action])
                
    policy = {state:np.argmax(actions) for state, actions in Q.items()}
                
    return policy, Q

policy, Q = every_visit_mc_control_const_alpha(env, 500000)

# obtain the corresponding state-value function
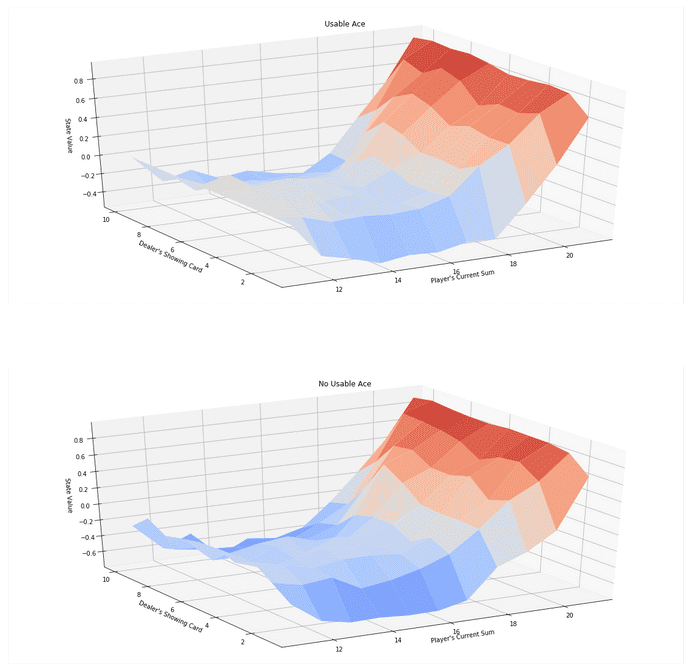
V_to_plot =  {state: np.max(actions) for state, actions in Q.items()}

# plot the state-value function
plot_blackjack_values(V_to_plot)

Progress:499000/500000